Talk:2021-04-23 53 9

I am sure you can calculate the probability yourself, but anyway here is my approximation:

Consider a circle of radius r at latitude θ and longitude ϕ. In the latitude/longitude coordinate space, if the circle is small (r ≪ graticule dimensions), it will look like an ellipse with semi-major axis ϕ_r and semi-minor axis θ_r. The semi-major axis will always be longitudinal due to the non-square shapes of the graticules. The lengths of the axes are:

ϕ_r = 1° × r / w_grat,

θ_r = 1° × r / h_grat,

where w_grat and h_grat are the width and the height of the graticule respectively at the centre point of the ellipse. Assuming that the Earth is a sphere with radius R = 6371000 m and taking θ = 53.6401767° from 2021-04-10_53_9, the dimensions of the graticule are approximately

h_grat = π R / 180 = 111195 m,

w_grat = h_grat cos θ = 65922 m.

Now, if r = 384 m, we get the axes of the ellipse:

ϕ_r = 0.00583°,

θ_r = 0.00345°.

The probability P₁ that a random hashpoint hits this ellipse is simply the area of the ellipse divided by the area of the graticule:

P₁ = (π ϕ_r θ_r) / (1° × 1°) = 6.32 × 10⁻⁵ = 1 / 15800.

Finally, the probability P₂ that a hashpoint hits the ellipse at least once in 13 days is

P₂ = 1 − (1 − P₁)¹³ = 8.21 × 10⁻⁴ = 1 / 1220.

An event of this probability will happen on average about once in 3.33 years or three years and four months.

― Kripakko (talk) 13:21, 24 April 2021 (UTC)

Wow, thanks for your calculations! I just used the area of my graticule, which I once calculated as 7299 km² (for spherical Earth), and then worked with ratios, but you actually put in the work with the ellipsis, and I suppose yours is more accurate, though we both disregarded that graticules are actually not rectangular. Anyway, I get (approximately) once in 7299/(0.384²*π*13) days = 3.32 years on average (3.33 with your calculated graticule area).

However, I don't visit every hash, so the probability of it happening for one of the geohashes I've been to this far (and could visit again) is only 1-(1-0.384²*π*13/7299)^76 = 6.1%. That's actually more than I expected! So for equal odds of it happening I'd have to do log(base 1-0.384²*π*13/7299)(0.5) = 840 hashes, which at my current pace would take me about 2.87+(840-78)/37 = 23.5 years total! I don't actually know if my method of calculating these is valid, but it makes sense to me. I just made the formulas up on the spot, since I don't really have any stochastical education.

I love that you're nerdy enough to calculate these as well. I was quite sure you'd notice this as you were the only other geohasher apart from Fippe who went on an expedition on 2021-04-10. Can I put your calculations on the expedition page? I think they'll be more appreciated there. --Π π π (talk) 10:10, 25 April 2021 (UTC)

Sure, go ahead and put the calculations on the expedition page. I am no mathematician nor statistician either, but I do mostly know what I am doing.

I did actually consider the non-rectangular shapes of the graticules. This is why is used the latitude/longitude coordinate space, and also since in that space the hashpoints are uniformly distributed, I could reason to myself that the calculations were valid. Of course, due to the non-rectangular graticule shape, the ellipse is not exactly an ellipse, but it is a good approximation when the radius of the circle is small.

Then, to make the calculations even more accurate, one could use the WGS84 ellipsoid to calculate the dimensions of the graticule. This is a much more complicated task, but fortunately there are tools for that, for example GeoCalcing². Using it, I got h_grat = 111296 m and w_grat = 66139 m for 2021-04-10_53_9 and finally P₂ = 8.18 × 10⁻⁴ = 1 / 1220. Not really a significant difference.

I cannot see anything wrong with your calculations, except for the "once in 7299/(0.384²*π*13) days = 3.32 years". You are not supposed to simply multiply the probability of an event when you calculate the probability of the event happening once in a number of times. If you do that with a large enough multiplier, you end up with a probability greater than one, which is obviously wrong. In this case, the probability and the multiplier are so small that the error is negligible, but it is incorrect in principle. You have got the right idea in the next expression with the 76th power though.

― Kripakko (talk) 12:35, 25 April 2021 (UTC)

Yeah I know, but the difference is so small that I didn't bother, that's why I said approximately. Also, I don't think it needs to be exactly once in this instance, at least once would suffice, but that depends on what exactly you want to calculate.

Wouldn't, for a given distance, the axes of the ellipse (in degrees) be different in the northern and southern parts of the graticule, since its northern boundary is shorter than its southern one (consider, for example, a graticule adjacent to the north pole)? So a hash would have a bigger probability per area in the northern part of the graticule, and therefore such an event should be more likely there. I don't see how that's represented in your calculations, since with defining w_grat = 65922 m it seems to me you assumed a rectangular graticule. The hashes are uniform in grid space, but 384 m is a distance in cartesian coordinates. That's why my result, using your graticule dimensions, is exactly the same as yours: π*384²/(111195*65922) = 6.3197e-5, using a circle instead of an ellipsis – it's the same calculation. From that point of view, I don't see the advantage of using ellipses. But there might be a flaw in my reasoning.

If, say, graticules were redefined as being between .5 in the latitudes (e.g. 53.5° to 54.5°), your calculated probability wouldn't change, but the actual probability would, I think, because the circle in coordinate space now takes up a different fraction of the graticule area in grid space. I haven't thought hard enough about this.

Of course, all these calculations disregard that because the Earth is curved, a graticule isn't trapezoidal either, and you'd probably at least have to use solid angles. And then there's the Earth spheroid …

Anyhow, I love calculating there kinds of things. Btw, have you heard about the Geohashing Discord? --π π π (talk) 20:13, 25 April 2021 (UTC)

Whoa, what a rabbit hole have I gone down after I started fiddling with this. It is all good fun of course but surprisingly time-consuming. :)

My bad, what I always meant and calculated was "at least once". Mostly because that is the easiest to calculate.

Perhaps I was not clear enough: my w_grat is the width of the graticule at the geohash latitude, so it is different in the southern and northern parts of the graticule. This does indeed mean that probability density is slightly higher in the north, and this is why the cos θ is there in my spherical approximation. My calculation accounts for that effect. Though the shape of a graticule is close enough to a rectangle that disregarding it will only cause a negligible error unless we are near the poles. So I guess there is no significant advantage, but I felt it was cleaner and more reasonable to myself that way. You are right in that respect.

A good point and something I just realised: since the longitudinal lines are not straight (except for the equator), the northern and southern edges of the graticules (I know, there are certain exceptions) are not straight either, and the graticules are not trapezoidal. This might become an issue near the poles, but at inhabitable latitudes I believe this can be ignored, and the error should be negligible when considering small areas.

The Earth spheroid is a pain to deal with, and after trying long enough to calculate the graticule dimensions easily (requires finding the length of an ellipse arc which is not possible analytically), I gave up and went for the spherical approximation. It is probably the largest error source though, so doing the other parts of the calculation overly correctly is futile unless one gets the correct dimensions from elsewhere like I did in the previous post. Furthermore, the ellipsoidal curvature just blows my mind when I try to think how to account for that, and I do not even know how large an error the spherical approximation causes there. Probably negligible in an area as small as a graticule.

Thanks for mentioning the server, I have not noticed it before. I am not very active on Discord, but I will check it out later.

― Kripakko (talk) 22:28, 25 April 2021 (UTC)

No, that was clear. But I don't see how that doesn't make the assumed graticule non-rectangular, as you still only have one width. It only seems to make it non-square. And I tried to explain above that I think you also need to account for how northern a hash is in a graticule.

What I was trying to understand is: You calculate P₁ = πϕ_rθ_r = πr² / (w_grath_grat) (leaving out the 1° factors) – that's the same calculation I did, though I had different graticule dimensions. I can't see how they differ, the calculation and results (using your dimensions) are exactly the same. Am I missing something?

Of course, all these small corrections are negligible in this case. I'm not sure if the spheroid would be the largest error source, since the difference in radii is only 0.17%, but that's hard to estimate for me. I also wouldn't be able to calculate that without looking it up somewhere, I'm having enough trouble mentally transforming from simple curved coordinate spaces. But it's interesting!

Welcome to the Discord! --π π π (talk) 21:27, 26 April 2021 (UTC)

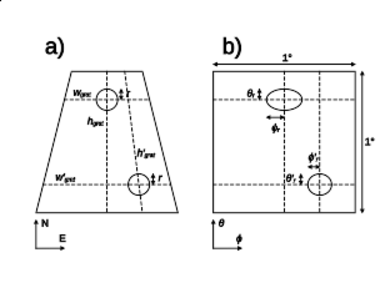A graticule of the northern hemisphere in (a) Cartesian space (rough, exaggerated shape) and (b) in latitude/longitude space. Two circles of the same radius r at different latitudes are transformed to ellipses with different semi-major axes ϕ_r and ϕ′_r and equal semi-minor axes and thus different areas. Since the hashpoint probability density is uniform in latitude/longitude space, the circles have different probabilities of containing a hashpoint. The heights h_grat and h′_grat are actually equal due to the curvature of the Earth, and so θ_r = θ′_r.

All right, I will try once more. It seems to me that you are not realising that the latitude affects the area of the ellipse. Here is a simplified and exaggerated picture of the situation. The circles are not circles in the latitude/longitude coordinate space, instead they need to be stretched so that the axes cover the same proportions of the width and the height of the graticule as in reality. And since the width of the graticule decreases closer to the poles, the major axes and also the areas of the ellipses must increase. Furthermore, since the hashpoints are distributed uniformly in this space, the ellipse with the larger area (the circle closer to the pole) has a larger probability of containing a hashpoint. Of course, the effect in reality is not nearly as large as in the figure, but it is there.

This effect is accounted for by the cos θ in my calculations. The formula that you presented is, when the spherical Earth approximation is used, actually P₁ = πr² / (h_grat² cos θ). This value changes when the latitude θ changes. In my opinion, it is not meaningful to say that I am calculating the area of the graticule, rather the coordinate transformation results in a calculation that looks like it. I do not know how to express this formally though, so do not take my words too literally.

I realise that I am not the best at explaining stuff while trying to be brief. I would have to write a thorough document explaining each bit of the thought process, but it would take way more time than this and it would be of interest for a handful of people, so I do not feel like being bothered to do that.

― Kripakko (talk) 11:31, 30 April 2021 (UTC)

Thanks for the explanation, but all that was very clear to me. I didn't question your approach of using ellipses, it's obviously correct. My remark was rather about the cos θ and there being no difference between our calculations when using the same graticule dimensions (which include the cos θ part). You only use cos θ to calculate the width of the graticule, but in your explanation you say that it accounts for the graticule being non-rectangular. But if you used a rectangular graticule, like I did, and a circle instead of an ellipse, you would still need the cos θ for calculating the graticule width. That's why the calculations are identical. Even in a non-square rectangular graticule, a circle in cartesian coordinates corresponds to an ellipse in grid space.

Your explanations are great, but it seems you misunderstood what I was wondering about. Anyway, I'm not sure this conversation is useful for much longer, so it would be all right with me if we abandoned it unless you have a new insight. But we could also continue, I don't mind. Online conversations like this are sometimes arduous because they take so long, while they could be resolved in a couple minutes if you talked face to face. --π π π (talk) 21:49, 1 May 2021 (UTC)

Ok, now I understand what you mean. I guess we just misinterpreted each other, and us both writing in not our native languages (ich glaube, dass du deutschsprachig bist) does not help. I agree that we can end this discussion since it is not really fruitful at this point. We can chat about something else somewhere else.

― Kripakko (talk) 13:21, 2 May 2021 (UTC)