Difference between revisions of "Algoritm"
imported>Llavids m |
m (Category) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
Du behöver inte förstå detta för att kunna ge dig ut på geohashäventyr. | Du behöver inte förstå detta för att kunna ge dig ut på geohashäventyr. | ||
| − | * Dagens datum i formatet | + | * Dagens datum i formatet åååå-mm-dd och det dagliga öppningspriset av [[Dow Jones Industrial Average]] (enligt [http://finance.google.com/finance?cid=983582 finance.google.com]) sätts ihop, med ett bindestreck emellan. |
| − | ** '''Väster om 30° västlig grad:''' Om det inte finns | + | ** '''Väster om 30° västlig grad:''' Om det inte finns något öppningspris från Dow Jones den dagen används priset från föregående aktiva dag istället. |
** '''Öster om 30° västlig grad:''' Samma som väster, fast gårdagens pris används, oavsett om ett nytt blir tillgängligt senare på dagen i just den tidszonen. Det vill säga torsdag använder onsdagens öppning, fredag använder torsdagens och lördag till måndag använder fredagens öppningspris. ''(kolla [[30W Time Zone Rule]])'' | ** '''Öster om 30° västlig grad:''' Samma som väster, fast gårdagens pris används, oavsett om ett nytt blir tillgängligt senare på dagen i just den tidszonen. Det vill säga torsdag använder onsdagens öppning, fredag använder torsdagens och lördag till måndag använder fredagens öppningspris. ''(kolla [[30W Time Zone Rule]])'' | ||
| − | * Resultatet körs sedan genom den väldokumenterade kryptografialgoritmen [[wikipedia:MD5|MD5]] för att generera en pseudoslumpmässig (men ändå lätt | + | * Resultatet körs sedan genom den väldokumenterade kryptografialgoritmen [[wikipedia:MD5|MD5]] för att generera en pseudoslumpmässig (men ändå lätt verifierad) "hash" bestående av 32 hexadecimala siffror. |
* Hashen delas sedan upp i två delar med 16 siffror vardera. | * Hashen delas sedan upp i två delar med 16 siffror vardera. | ||
* Varje del får ett komma framför sig (så det blir ett decimaltal) och konverteras till basen 10. | * Varje del får ett komma framför sig (så det blir ett decimaltal) och konverteras till basen 10. | ||
| Line 15: | Line 15: | ||
* '''Online md5() generator''' | * '''Online md5() generator''' | ||
** [http://www.iwebtool.com/md5 iWebTool.com] | ** [http://www.iwebtool.com/md5 iWebTool.com] | ||
| − | ** [http:// | + | ** [http://carabiner.peeron.com/cgi-bin/md5.cgi carabiner.peeron.com] |
* '''Beräkning av bråk, hexadecimal till basen 10''' | * '''Beräkning av bråk, hexadecimal till basen 10''' | ||
** [http://www.easysurf.cc/cnver17.htm#bf16tobf10 EasySurf.cc] | ** [http://www.easysurf.cc/cnver17.htm#bf16tobf10 EasySurf.cc] | ||
| Line 28: | Line 28: | ||
* Däremot leder interaktionen mellan den 180:e meridianen och den internationella datumlinjen till en del intressanta observationer. Där de bryter varandra kan upp till tre hashpunkter vara väldigt nära varandra, till och med långt ifrån ekvatorn. Om man står precis väst om 180E, lite lite öster om datumlinjen så kan man vara på hashen till 179E från "idag" med hashen för 179E "imorgon" precis väster om dig och hashen för "idag" i 179W precis öster om dig. Chansen att få tre olika slumpmässiga koordinater att komma nära varandra på detta sätt är av en helt annan magnitud än det förra fallet. | * Däremot leder interaktionen mellan den 180:e meridianen och den internationella datumlinjen till en del intressanta observationer. Där de bryter varandra kan upp till tre hashpunkter vara väldigt nära varandra, till och med långt ifrån ekvatorn. Om man står precis väst om 180E, lite lite öster om datumlinjen så kan man vara på hashen till 179E från "idag" med hashen för 179E "imorgon" precis väster om dig och hashen för "idag" i 179W precis öster om dig. Chansen att få tre olika slumpmässiga koordinater att komma nära varandra på detta sätt är av en helt annan magnitud än det förra fallet. | ||
* Datumlinjen kan också göra så att en enda kvadrant kan innehålla två (eller inga) hashpunkter vid en given tidpunkt beroende på vilken sida av linjen punkterna för de två dagarna hamnar. Detta kan hända var som helst som linjen delar en kvadrant i två. | * Datumlinjen kan också göra så att en enda kvadrant kan innehålla två (eller inga) hashpunkter vid en given tidpunkt beroende på vilken sida av linjen punkterna för de två dagarna hamnar. Detta kan hända var som helst som linjen delar en kvadrant i två. | ||
| − | * Kvadranter är som mest kvadratiska vid ekvatorn medan de vid polerna är ungefär 2 km * 111 km höga trianglar. Om du lyckas besöka någon av polerna, vilket i sig själv bevisar att "[[MNIMB_Geohash|Mother Nature Is Your Bitch]]" så borde du kunna besöka väldigt många kvadranter inom | + | * Kvadranter är som mest kvadratiska vid ekvatorn medan de vid polerna är ungefär 2 km * 111 km höga trianglar. Om du lyckas besöka någon av polerna, vilket i sig själv bevisar att "[[MNIMB_Geohash|Mother Nature Is Your Bitch]]" så borde du kunna besöka väldigt många kvadranter inom en väldigt kort tidsrymd. På grund av 30W-regeln kommer hashpunkterna vara delade i två delar som utgör ojämna halvor av två olika stora 360-goner. I värsta fall måste man resa 700 km för att besöka alla 360 punkter, medan de rent teoretiskt kan hamna hur nära varandra som helst (28 juli 2008 var värdena 0,985 och 0,855, vilket satte 150 punkter bara 4,4 km ifrån varandra vid nordpolen och de resterande 210 längs en lite större 59 km båge bara 14,4 km bort. Det hade räckt att resa 78 km för att nå dem alla!). |
'''Q:''' Jag försökte använda min md5sum från unit/linux kommandoprompt och hashen var inte samma som serien. Vad är korrekt? | '''Q:''' Jag försökte använda min md5sum från unit/linux kommandoprompt och hashen var inte samma som serien. Vad är korrekt? | ||
| Line 37: | Line 37: | ||
== Implementationer == | == Implementationer == | ||
| − | Om du inte vill göra beräkningarna själv så behövs det inte. | + | Om du inte vill göra beräkningarna själv så behövs det inte. En lista med referenser och praktiska implementationer finns på [[Implementations|implementationssidan]]. |
== Kända problem == | == Kända problem == | ||
| Line 47: | Line 47: | ||
[[Category:Algorithm]] | [[Category:Algorithm]] | ||
| − | [[Category:Swedish | + | [[Category:Pages in Swedish]] |
Latest revision as of 12:21, 10 January 2022
Den här gången var det vi som uppfann algoritmen!
Du behöver inte förstå detta för att kunna ge dig ut på geohashäventyr.
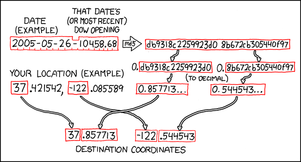
- Dagens datum i formatet åååå-mm-dd och det dagliga öppningspriset av Dow Jones Industrial Average (enligt finance.google.com) sätts ihop, med ett bindestreck emellan.
- Väster om 30° västlig grad: Om det inte finns något öppningspris från Dow Jones den dagen används priset från föregående aktiva dag istället.
- Öster om 30° västlig grad: Samma som väster, fast gårdagens pris används, oavsett om ett nytt blir tillgängligt senare på dagen i just den tidszonen. Det vill säga torsdag använder onsdagens öppning, fredag använder torsdagens och lördag till måndag använder fredagens öppningspris. (kolla 30W Time Zone Rule)
- Resultatet körs sedan genom den väldokumenterade kryptografialgoritmen MD5 för att generera en pseudoslumpmässig (men ändå lätt verifierad) "hash" bestående av 32 hexadecimala siffror.
- Hashen delas sedan upp i två delar med 16 siffror vardera.
- Varje del får ett komma framför sig (så det blir ett decimaltal) och konverteras till basen 10.
- Dessa decimaltal läggs till heltalsvärdena (latitud och longitud) för varje given kvadrant och bildar därmed dagens resmål.
Beräkningshjälp
- Online md5() generator
- Beräkning av bråk, hexadecimal till basen 10
- Pris från Dow Jones
- De som vill fånga öppningspriset direkt från finance.google.com kan använda märkningen:
<span id="ref_983582_op">99,999.99</span> - Andra källor finns på Dow Jones Industrial Average.
- De som vill fånga öppningspriset direkt från finance.google.com kan använda märkningen:
Särdrag
Det finns ett antal resultat vid applicerande av algoritmen som kanske inte är uppenbara vid en första anblick, men som innebär intressant tankeexperiment och kanske ännu mer intressant bedrifter vid bizarra eller äventyrliga scenarier.
- Koordinaterna vid den första meridianen är speglade istället för att följa rutmönstret. Det innebär att ett lågt longitudvärde (säg 0,001) kan göra så att två punkter hamnar väldigt nära varandra på varsin sida om 0°. Här borde det var 111:e dag bli två punkter inom en kilometer ifrån varandra. Ekvatorn har samma fenomen, och skärningen mellan dessa kan göra att fyra punkter hamnar väldigt nära varandra. Detta är tyvärr mitt ute i Atlanten.
- Den 30W och den 180:e meridianen är inte lika speciella, de har helt enkelt helt oberoende punkter. De kan vara godtyckligt nära varandra eller upp till två kvadrantdiagonaler ifrån varandra. De interagerar med ekvatorn på samma sätt som ovan.
- Däremot leder interaktionen mellan den 180:e meridianen och den internationella datumlinjen till en del intressanta observationer. Där de bryter varandra kan upp till tre hashpunkter vara väldigt nära varandra, till och med långt ifrån ekvatorn. Om man står precis väst om 180E, lite lite öster om datumlinjen så kan man vara på hashen till 179E från "idag" med hashen för 179E "imorgon" precis väster om dig och hashen för "idag" i 179W precis öster om dig. Chansen att få tre olika slumpmässiga koordinater att komma nära varandra på detta sätt är av en helt annan magnitud än det förra fallet.
- Datumlinjen kan också göra så att en enda kvadrant kan innehålla två (eller inga) hashpunkter vid en given tidpunkt beroende på vilken sida av linjen punkterna för de två dagarna hamnar. Detta kan hända var som helst som linjen delar en kvadrant i två.
- Kvadranter är som mest kvadratiska vid ekvatorn medan de vid polerna är ungefär 2 km * 111 km höga trianglar. Om du lyckas besöka någon av polerna, vilket i sig själv bevisar att "Mother Nature Is Your Bitch" så borde du kunna besöka väldigt många kvadranter inom en väldigt kort tidsrymd. På grund av 30W-regeln kommer hashpunkterna vara delade i två delar som utgör ojämna halvor av två olika stora 360-goner. I värsta fall måste man resa 700 km för att besöka alla 360 punkter, medan de rent teoretiskt kan hamna hur nära varandra som helst (28 juli 2008 var värdena 0,985 och 0,855, vilket satte 150 punkter bara 4,4 km ifrån varandra vid nordpolen och de resterande 210 längs en lite större 59 km båge bara 14,4 km bort. Det hade räckt att resa 78 km för att nå dem alla!).
Q: Jag försökte använda min md5sum från unit/linux kommandoprompt och hashen var inte samma som serien. Vad är korrekt?
- A: Du glömde antagligen "-n" (echo utan ny rad). Testa detta för att matcha exemplet:
echo -n 2005-05-26-10458.68 | md5sum- Kommandot md5sum kan också kallas md5.
Implementationer
Om du inte vill göra beräkningarna själv så behövs det inte. En lista med referenser och praktiska implementationer finns på implementationssidan.
Kända problem
Flera kända problem listas här. Det finns en pågående diskussion om dessa och flera andra här: Talk:Main Page.
Slumpmässighet
Några personer har ifrågasatt algoritmens slumpmässighet. För att analysera denna fråga skrevs ett litet python program som använder algoritmen för att skjuta på ett fönster genom att göra träffade pixlar röda. Här är resultatet: Bakgrunden är svart, en pixel blir ljusare ju fler gånger den träffas. Om du ser någon som helst system eller ett mönster kolla på A Beautiful Mind och anmäl dig till en passande institution.