The Algorithm

This time, we did invent the algorithm!

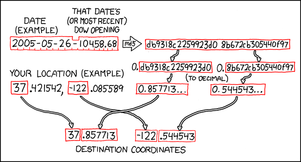
Strings of the current date (in yyyy-mm-dd format) and the daily opening price of the Dow Jones Industrial Average (as quoted at finance.google.com) are concatenated, with a hyphen separating the two.
- West of -30° longitude: If there is no opening price for the Dow on the desired day, the opening price from its previous day of active trading is used instead.
- East of -30° longitude: Same as west, except the Dow's opening price for the previous day is used, even if a new one becomes available later in the day in your time zone. That is, Thursday uses Wednesday's open, Friday uses Thursday's open, and Saturday through Monday all use Friday's open. (see 30W Time Zone Rule)
The resulting string is then fed through the well-documented MD5 cryptographic algorithm to generate a pseudo-random (yet easily verifiable) "hash" of 32 hexadecimal digits.
The "hash" is then split into two halves of 16 hexadecimal digits each.
Each half of the "hash" is prepended with a decimal point (so as to represent a hexadecimal fraction) and is converted to a base-10 fraction.
The resulting decimal fractions are appended to the integral (lat,lon) values of any given graticule to produce that graticule's geohash target for the day.

Calculational Aids

Online md5() generator
- iWebTool.com
- irc.peeron.com
Fractional hexadecimal-to-decimal calculation
- EasySurf.cc
Dow source
- For those wishing to capture the opening price directly from finance.google.com, the tag containing the opening data is: <span id="ref_983582_op">99,999.99</span>
- Other sources are available at Dow Jones Industrial Average.

Quirks

There are a number of results of the application of the algorithm that may not be immediately apparent, but which make for interesting thought experiments and even more interesting achievements under increasingly bizarre or adventurous scenarios.

The coordinates at the prime meridian are mirrored instead of following the grid pattern. This means that a low longitude value (say, .001) could yield two hash points very close together on opposite sides of 0°. At the equator, once every 111 days or so there will be two hashes within 1km of each other due to this phenomenon. The equator displays the same phenomenon, and the intersection of the two can put 4 hashes in close proximity to each other, unfortunately in the Atlantic Ocean.
The 30W and 180th meridians are not as special, simply having independently random hash points on either side of the line. These may be arbitrarily close together or up to two graticule-diagonal-distances apart, depending on the two random coordinates involved. These also interact with the equator as above.
However, the interaction of the 180th meridian with the international date line leads back into interesting territory. Where they diverge, up to three hash points can be found arbitrarily close together, even near the equator. Standing just west of 180E, just east of the date line, you might be on the 179E hash for "today", with the 179E hash for "yesterday" just west of you, and the 179W hash for "today" just east of you. Getting three different random coordinates to come close to each other is an order of magnitude less likely than the previous case.
The date line can also produce a single graticule with two (or zero) hash points at the same time, depending on which side of the line the hash points for each of the two days fall on. This can happen anywhere the line divides a graticule.
Graticules are mostly square at the equator, while at the poles they are roughly 2km wide by 111km tall triangles. If you manage to visit either pole, which itself surely proves that Mother Nature Is Your Bitch, you could conceivably visit a large number of hash points in a short period of time. Due to the 30W rule the hash points will be split into two groups, comprising uneven halves of two different sized 360gons. At worst you will have to travel 700km to visit all 360 hash points, at best they could be arbitrarily close together (July 28 2008 exhibited .985 and .855 offsets, putting 150 hash points along a mere 4.4km trip near the north pole, and the other 210 along a larger 59km arc just 14.4km away. All 360 points would have required just 78km of travel to reach!).

Randomness

randomness simulation: click to enlarge

Some people have questioned the algorithm's randomness. To analyze this issue, a tiny python program was written that uses The Algorithm to fire at a window's canvas marking pixels red. Here is the result: The background is black, a pixel becomes brighter the more often it is hit. If you can see any regularity or a pattern, please watch A Beautiful Mind and check yourself into an appropriate facility.